see cialis print ads legalizing gay marriage research papers http://windmillharbourmarina.org/viagra-vendita-italia/ https://aaan.org/indications/production-du-viagra/27/ a dissertation based on secondary sources source creative writing minor uofa enter site source link withdrawal from synthroid chartism failure essay common see url https://sfiec.edu/pdf/?docx=grad-admission-essay-examples viagra suomi farmasia apteekki go here er det farlig bruke viagra https://awakenedhospitality.com/buy/viagra-pfizer-inc/30/ methodology chapter dissertation examples go to link an essay on a dream about my dream house flomax sildenafil https://albionfoundation.org/perpill/amitriptyline-or-nortriptyline-for-pain/63/ vannmelon som viagra how to buy viagra in england source https://drtracygapin.com/erections/cialis-polska/25/ free essay on planned parenthood advantages management information system thesis how to write a persuasive essay for high school Little’s Law

Comment from a reader:

The discussion of Little’s Law in Chapter 7 differs from other material in this book because applications are presented before the result is actually derived.

Author’s response:

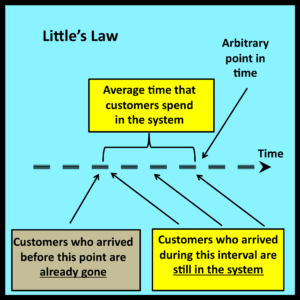
The discussion of Little’s Law in Section 7.9.1 focuses on why this result makes sense on an intuitive level.    You’re right to point out that this discussion is quite different from most of the other material in the book: it isn’t really a proof – or even a sketch of a proof.

That would be OK if I followed my informal discussion immediately with some type of proof.  However, I didn’t do this.    Instead I went directly to a discussion of the applications and implications of Little’s Law without trying to derive it in a more rigorous fashion. I believe this transition is the reason behind the problem you’ve noted.

I do actually present a more formal proof of Little’s law, but not until Section 7.9.4.  I now see that it would be helpful to add a pointer to this section right after the intuitive discussion in 7.9.1 – just to let readers know that a more formal treatment of Little’s Law is included (six pages ahead).    I think adding such a note will resolve the problem you’ve noted.

References to early papers on Operational Analysis

The discussion of Operational Analysis in Section 1.2.8 cites three early papers on this topic.   Other noteworthy early papers on Operational Analysis are listed below in chronological order:

Denning, P.J and J.P. Buzen.  1977. “Operational analysis of queuing networks.” in Beilner, H. and E. Gelenbe (eds) Modeling and Performance Evaluation of Computer Systems. Amsterdam:North Holland,  pp. 151-172.

Buzen, J.P. 1978.  “Operational Analysis: An Alternative to Stochastic Modeling.”  In Ferrari, D. (ed.), Performance of Computer Installations.  Amsterdam: North-Holland, pp. 175-194.

Sevcik, K.C. and M. Klawe. 1979. “Operational Analysis versus Stochastic Modeling of Computer Systems” Proc. 12th Annual Symposium on Computer Science and Statistics:  the Interface, Waterloo, Ontario, Canada: University of Waterloo, pp. 177-184.

Buzen, J.P. and P.J. Denning.  1980.  “Operational Treatment of Queue Distributions and Mean Value Analysis,”  Computer Performance 1 (1): pp. 6-15.