Non-Parametric Statistics

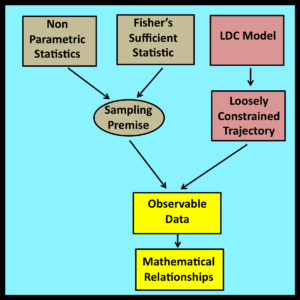
Results derived through non-parametric statistics are typically characterized as being “distribution free.” In other words, they are based on the assumption that observed values have been drawn “at random” from underlying probability distributions whose exact form has no influence on the analysis. Thus, non-parametric statistics still relies to some degree on the sampling premise.

Perhaps an alternative starting point for non-parametric statistics is to simply assume that observed values are immaterial details subject to loose constraints. This might lead to simpler derivations of certain results, a more direct connection between derived results and observable properties of the real world, and new forms of sensitivity/risk analysis.

A good starting point for this investigation would be a careful examination of Chebyshev’s inequality.

Fisher’s Sufficient Statistic

In observational stochastics, loose constraints are sufficient to ensure that derived results are valid. R A Fisher’s notion of a sufficient statistic (see Wikipedia) appears to provide a similar guarantee. Is there a relationship? (My thanks to Professor Donald B Rubin of Harvard for raising this issue during an animated dinner conversation.)