9.1 The Law of Large Numbers

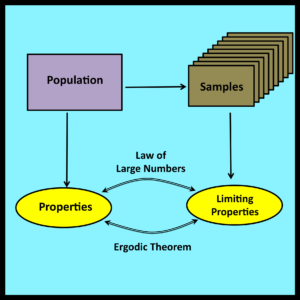
The Law of Large Numbers establishes a linkage between the observable properties of random samples and the properties of underlying populations from which such samples are drawn.  The next few sections provide a proportionalist interpretation of this well known and fundamentally important result.

As usual, it is helpful to begin with a simple example. Suppose an urn contains a number of colored balls.  An experimenter reaches into the urn, selects a ball at random, notes its color and then returns the ball to the urn.  Assume this basic sampling procedure is repeated for a total of N cycles.

Let
k   = total number of balls in the urn

g   = number of balls in the urn that are green

N  = number of sampling cycles (i.e., number of times a ball is drawn from the urn and then replaced)

If N is large, it is reasonable to expect that the fraction of green balls in the N samples should be close to the fraction of green balls in the urn itself.  Since g/k is the fraction of green balls in the urn, it follows that the total number of green balls drawn during the experiment should be approximately equal to Nx(g/k).

This result cannot be guaranteed with certainty because of the random nature of the sampling process.  However, its validity should become increasingly likely as the value of N grows larger.  The Law of Large Numbers provides a mathematically rigorous characterization and proof of this intuitively appealing notion.

*
*
*

9.2 The Ergodic Theorem

The Law of Large numbers deals with the relationship between the observable properties of large numbers of random samples and the properties of the underlying population from which these samples are drawn.  The Ergodic Theorem also deals with relationships between samples and underlying populations, but in this case the samples are not statistically independent and the populations have complex structures that cannot be represented as urns containing finite numbers of balls of various colors.

Despite these differences, the Ergodic Theorem and the Law of Large Numbers both lead to conclusions that make good sense on an intuitive level: they both imply that important observable properties of samples will, in the limit, approach the corresponding properties of the underlying population.  However, these conclusions are substantially more difficult to characterize rigorously in the case of the Ergodic Theorem because the term “in the limit” cannot be interpreted in the conventional manner. The next few sections examine the reasons these difficulties arise and the formalisms that have been devised to overcome them.

*
*
*

9.2.7 Role of measure theory

The Ergodic Theorem deals with the properties of ergodic stochastic processes. Each of these processes has a steady state distribution and is associated with an ensemble (i.e., a set) of associated trajectories. Essentially, the Ergodic theorem states that trajectory-based proportions will, in almost all cases, converge to the steady state distribution of the associated stochastic process as the length of the trajectory approaches infinity.

Note that convergence is not guaranteed. Some trajectories associated with an ergodic stochastic process may fail to converge. The main technical challenge in the proof of the Ergodic Theorem is to show that these non-convergent trajectories represent a negligible fraction of the entire ensemble and can be safely ignored. Measure theory provides a set of tools and formal concepts that can be used to demonstrate this point.

The key to the proof of the Ergodic Theorem is the concept of Borel measure, developed by Émile Borel to characterize the total length (i.e., the measure) of any given subset of the real line. In general, each subset is comprised of segments and individual discrete points. If the number of segments and points is finite, Borel’s method and the straightforward measurement procedure described in Section 3.7.4 yield exactly the same results. However, Borel’s definition also accommodates difficult cases where the number of segments and/or the number of points may be infinite. Under Borel’s characterization, the measure of such a subset can be zero even though it contains an infinite number of members.

George Birkhoff’s celebrated proof of the Ergodic Theorem [Birkhoff 1931] is based on an unexpectedly powerful application of the concept of Borel measure. Specifically, Birkhoff demonstrated that the set of non-convergent trajectories (i.e., trajectories whose observable proportions do not converge to the steady state distribution of the associated stochastic process) has Borel measure zero. Thus, in order to appreciate the strengths and limitations of the Ergodic Theorem, it is important to understand what it means for a set to have “measure zero”.

Essentially, the Borel measure of any set of discrete points or continuous intervals is the combined length of the smallest set of non-overlapping intervals that cover (i.e., contain) these points or intervals completely. This intuitively appealing notion of covering the set being measured by another set of intervals and then shrinking the lengths of the covering intervals to their minimum size is the central principle behind Borel’s notion of measurement.

The length of each interval in the covering set is computed, as described in Section 3.7.4, by subtracting its starting position from its ending position. The combined length of all covering intervals is then computed by a summation that may involve an infinite number of terms. If the sum converges to a well-defined limit, that limiting value is the Borel measure of the original set.

If, for every epsilon greater than zero, it is possible to find a set of non-overlapping covering intervals whose combined length is less than or equal to epsilon, then the Borel measure of this set is equal to zero. This procedure for characterizing sets of “measure zero” is the crown jewel of Borel measure and a pillar of modern measure theory. In probability theory, which can be regarded as a special application of measure theory, an event is said to occur with “probability zero” if its Borel measure is zero. Similarly, an event is said to occur “almost surely” if its Borel measure is equal to one (i.e., if its complement has measure zero).

One of the best known examples of a set of measure zero is the set of rational numbers in the interval [0,1]. Even though this set contains an infinite number of members, the set is still countable as defined by the nineteen century mathematician Georg Cantor. This means its members can be arranged to form a simple linear sequence as shown in equation (9-13).

Set of rational numbers in [0,1] =
{0,1,1/2, 1/3, 2/3, 1/4, 3/4, 1/5, 2/5, 3/5, 4/5 , 1/6, 5/6, … } (9-13)

The first member of this sequence can be covered by an interval of length epsilon/2, the second by an interval of epsilon/4, the third by an interval of length epsilon/8, and so on. The sum of the lengths of this infinite sequence of partially overlapping covering intervals, which clearly represents an upper bound on the set’s Borel measure, is equal to epsilon. Since epsilon can be made arbitrarily small, the Borel measure of the set of rational numbers in [0,1] must thus be equal to zero.

In the terminology of probability theory, if a number is drawn at random from the set of real numbers in the interval [0,1], it will “almost surely” be irrational. Drawing a rational number under these circumstances represents an event that occurs with “probability zero”. Although these conclusions are consistent with the mathematically precise definition of Borel measure, they may seem counter-intuitive to practitioners since the interval [0,1] actually contains an infinite number of rational numbers. Measure theory has many other implications that are also difficult to reconcile on an intuitive level (Gelbaum and Olmsted 1964).

A more exotic example of a set of measure zero is the Cantor set, also known as the Cantor ternary set. This set is constructed by systematically removing the open middle third of every closed interval in [0,1] ad infinitum. The first three removal cycles are depicted in Table 9-7. It is easy to show that the measure of the Cantor set is zero. However, this set is still fundamentally larger than the set of rational numbers. Technically, the Cantor set has the cardinality of the continuum and contains an uncountably infinite number of members, while the set of rational numbers in [0,1] has a lower cardinality and is merely countably infinite.

The existence of the Cantor set raises further concerns regarding the Ergodic Theorem. The fact that this theorem is “almost surely” valid for the trajectories in a given ensemble does not prevent the number of non-convergent trajectories within that ensemble from being uncountably infinite.

The Cantor set also has certain exceptional properties that are of special interest to mathematical theorists. For example, since the Borel measure of the Cantor set is zero, it is reasonable to expect that all subsets of the Cantor set must also have measure zero. However, this is not so: some subsets of the Cantor set are not Borel measurable.

Borel’s student Henri Lebesgue refined Borel’s original definition of measure to ensure that all subsets contained within a set of measure zero are also measurable and also have measure zero. This refinement is known as Lebesgue measure. In technical terms, Lebesgue measure represents the completion of Borel measure.

Even after the process of completion, a modicum of untidiness remains. In particular, it is not true that all subsets of a Lebesgue measurable set are Lebesgue measurable. This intuitively appealing relationship is, in fact, only valid for sets of measure zero.

Lebesgue’s work had a powerful influence on Kolmogorov, whose formulation of the axiomatic theory of probability “would have been a rather hopeless…task…before the introduction of Lebesgue’s theories of measure and integration” (Kolmogorov 1933). As a result, many crucial results in modern probability theory are only valid for sets that are Lebesgue measurable. This constraint, which is required to rule out certain unusual counter-examples, has little if any practical impact: the finite sets of observations that practitioners deal with are always Lebesgue measureable.