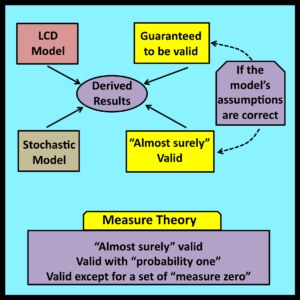
 Observational stochastics deals directly with observable properties of individual trajectories whose lengths are finite. This makes it possible to analyze such properties without appealing to the Law of Large Numbers or the Ergodic Theorem. As a result, none of the formalities and subtle mathematical complexities discussed in Chapter 9 ever arise. There is no need to consider concepts such as Lebesgue measurability, sets of measure zero, and results that are almost surely, but not always, valid. The results derived through observational stochastics can be applied to directly observable quantities with complete certainty in all cases where the directly verifiable assumptions of the corresponding LCD model are satisfied.
Observational stochastics deals directly with observable properties of individual trajectories whose lengths are finite. This makes it possible to analyze such properties without appealing to the Law of Large Numbers or the Ergodic Theorem. As a result, none of the formalities and subtle mathematical complexities discussed in Chapter 9 ever arise. There is no need to consider concepts such as Lebesgue measurability, sets of measure zero, and results that are almost surely, but not always, valid. The results derived through observational stochastics can be applied to directly observable quantities with complete certainty in all cases where the directly verifiable assumptions of the corresponding LCD model are satisfied.
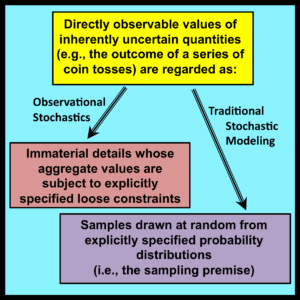
Although these benefits are of genuine value to practitioners, the most important contributions of observational stochastics are conceptual rather than pragmatic. At its core, observational stochastics provides an alternative framework for thinking about and analyzing the behavior of systems in situations that involve uncertainty and randomness. In such cases, traditional stochastic analyses begin by invoking the sampling premise: that is, by assuming that observed values can be regarded as samples that have been drawn at random from underlying probability distributions.
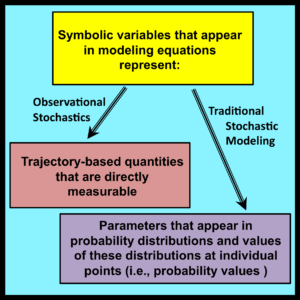
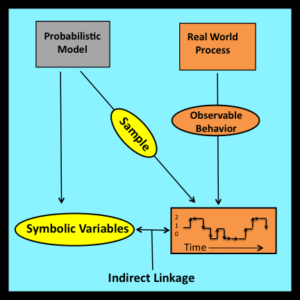 The sampling premise shifts the focus of the analysis to probability distributions and their parameters. As pointed out at the start of Chapter 1, a model based on these entities is incompatible with the observability principle, which requires that all symbolic variables used in a mathematical model must correspond to directly observable and measurable properties of the system being modeled.
The sampling premise shifts the focus of the analysis to probability distributions and their parameters. As pointed out at the start of Chapter 1, a model based on these entities is incompatible with the observability principle, which requires that all symbolic variables used in a mathematical model must correspond to directly observable and measurable properties of the system being modeled.
The exact meaning of directly observable and measurable is open to interpretation. However, it seems clear that this term is not applicable to quantities that can only be evaluated through procedures that require the Law of Large Numbers or the Ergodic Theorem for their formal justification.
The symbolic variables employed in observational stochastics are entirely different. By design, they are intended to represent quantities that are directly observable and measurable within the formal modeling framework developed in Section 3.7.
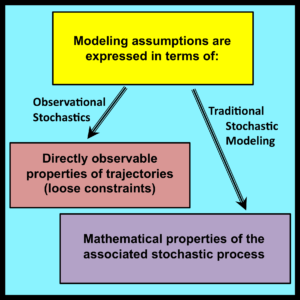
Observational stochastics must also provide a mechanism for representing uncertainty. This is achieved by regarding the directly observable and measurable values of uncertain quantities as immaterial details whose aggregate properties are subject to model-specific loose constraints. This alternative approach to the characterization of uncertainty sets observational stochastics apart from traditional stochastic modeling.
Note that the two modeling frameworks are not mutually exclusive. They simply provide alternative justifications for the validity of certain equations used to analyze the performance of real world systems. There is no reason why both justifications cannot be correct. Observational stochastics does offer practitioners a number of substantial advantages that have been detailed on the pages of this book. On the other hand, traditional stochastic modeling is a more mature discipline that has been applied successfully to many problems that are beyond the current scope of observational stochastics. It seems likely that both approaches will continue to yield useful and interesting results in the future.